Algebra Review Factoring and Trinomials and Sinplifying Rational Expressions Pachet

Prerequisites

Rational Expressions

Learning Objectives

In this section students will:

Simplify rational expressions.
Multiply rational expressions.
Divide rational expressions.
Add and subtract rational expressions.
Simplify complex rational expressions.

A pastry shop has fixed costs of $\,\text{\$}280\,$ per week and variable costs of $\,\text{\$}9\,$ per box of pastries. The shop's costs per week in terms of $\,x,$ the number of boxes made, is $\,280+9x.\,$ We can split the costs per calendar week by the number of boxes made to determine the cost per box of pastries.

$\frac{280+9x}{x}$

Notice that the consequence is a polynomial expression divided by a second polynomial expression. In this section, we volition explore quotients of polynomial expressions.

Simplifying Rational Expressions

The quotient of ii polynomial expressions is called a rational expression. Nosotros tin can apply the properties of fractions to rational expressions, such every bit simplifying the expressions by canceling common factors from the numerator and the denominator. To practise this, we first need to factor both the numerator and denominator. Permit's beginning with the rational expression shown.

$\frac{{x}^{2}+8x+16}{{x}^{2}+11x+28}$

Nosotros tin can factor the numerator and denominator to rewrite the expression.

$\frac{{\left(x+4\right)}^{2}}{\left(x+4\right)\left(x+7\right)}$

Then we tin simplify that expression past canceling the common factor $\,\left(x+4\right).$

$\frac{x+4}{x+7}$

How To

Given a rational expression, simplify it.

Factor the numerator and denominator.
Cancel any common factors.

Simplifying Rational Expressions

Simplify $\,\frac{{x}^{2}-9}{{x}^{2}+4x+3}.$

[reveal-respond q="fs-id1167339232113″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1167339232113″]

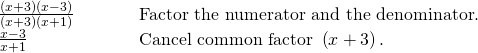$\begin{array}{lllll}\frac{\left(x+3\right)\left(x-3\right)}{\left(x+3\right)\left(x+1\right)}\hfill & \hfill & \hfill & \hfill & \text{Factor the numerator and the denominator}.\hfill \\ \frac{x-3}{x+1}\hfill & \hfill & \hfill & \hfill & \text{Cancel common factor }\left(x+3\right).\hfill \end{array}$ [/subconscious-reply]

Analysis

Nosotros tin can cancel the common factor because any expression divided past itself is equal to 1.

Tin the $\,{x}^{2}\,$ term be cancelled in (Figure)?

No. A factor is an expression that is multiplied by some other expression. The $\,{x}^{2}\,$ term is non a factor of the numerator or the denominator.

Try It

Simplify $\,\frac{x-6}{{x}^{2}-36}.$

[reveal-answer q="fs-id1167339126332″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1167339126332″]

$\frac{1}{x+6}$

[/subconscious-respond]

Multiplying Rational Expressions

Multiplication of rational expressions works the same way equally multiplication of any other fractions. We multiply the numerators to find the numerator of the product, and then multiply the denominators to find the denominator of the product. Earlier multiplying, it is helpful to factor the numerators and denominators just as nosotros did when simplifying rational expressions. We are often able to simplify the product of rational expressions.

How To

Given two rational expressions, multiply them.

Cistron the numerator and denominator.
Multiply the numerators.
Multiply the denominators.
Simplify.

Multiplying Rational Expressions

Multiply the rational expressions and show the product in simplest form:

$\frac{\left(x+5\right)\left(x-1\right)}{3\left(x+6\right)}\cdot \frac{\left(2x-1\right)}{\left(x+5\right)}$

[reveal-answer q="fs-id1167339228244″]Prove Solution[/reveal-answer]
[hidden-reply a="fs-id1167339228244″]

$\begin{array}{lllll}\frac{\left(x+5\right)\left(x-1\right)}{3\left(x+6\right)}\cdot \frac{\left(2x-1\right)}{\left(x+5\right)}\hfill & \hfill & \hfill & \hfill & \text{Factor the numerator and denominator}.\hfill \\ \frac{\left(x+5\right)\left(x-1\right)\left(2x-1\right)}{3\left(x+6\right)\left(x+5\right)}\hfill & \hfill & \hfill & \hfill & \text{Multiply numerators and denominators}.\hfill \\ \frac{\overline{)\left(x+5\right)}\left(x-1\right)\left(2x-1\right)}{3\left(x+6\right)\overline{)\left(x+5\right)}}\hfill & \hfill & \hfill & \hfill & \text{Cancel common factors to simplify}.\hfill \\ \frac{\left(x-1\right)\left(2x-1\right)}{3\left(x+6\right)} \hfill & \hfill & \hfill & \hfill & \hfill \end{array}$ [/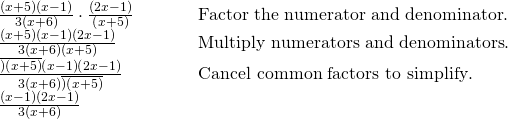hidden-respond]

Endeavor It

Multiply the rational expressions and show the production in simplest form:

$\frac{{x}^{2}+11x+30}{{x}^{2}+5x+6}\cdot \frac{{x}^{2}+7x+12}{{x}^{2}+8x+16}$

[reveal-respond q="fs-id1167339228097″]Testify Solution[/reveal-reply]
[subconscious-reply a="fs-id1167339228097″]

$\frac{\left(x+5\right)\left(x+6\right)}{\left(x+2\right)\left(x+4\right)}$

[/hidden-answer]

Dividing Rational Expressions

Sectionalization of rational expressions works the same way as sectionalization of other fractions. To dissever a rational expression by another rational expression, multiply the outset expression past the reciprocal of the 2d. Using this approach, we would rewrite $\,\frac{1}{x}÷\frac{{x}^{2}}{3}\,$ equally the product $\,\frac{1}{x}\cdot \frac{3}{{x}^{2}}.\,$ Once the division expression has been rewritten as a multiplication expression, we can multiply as nosotros did before.

$\frac{1}{x}\cdot \frac{3}{{x}^{2}}=\frac{3}{{x}^{3}}$

How To

Given two rational expressions, separate them.

Rewrite as the first rational expression multiplied by the reciprocal of the second.
Factor the numerators and denominators.
Multiply the numerators.
Multiply the denominators.
Simplify.

Dividing Rational Expressions

Carve up the rational expressions and express the quotient in simplest form:

$\frac{2{x}^{2}+x-6}{{x}^{2}-1}÷\frac{{x}^{2}-4}{{x}^{2}+2x+1}$

[reveal-respond q="fs-id1167339185775″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339185775″]

$\frac{9{x}^{2}-16}{3{x}^{2}+17x-28}÷\frac{3{x}^{2}-2x-8}{{x}^{2}+5x-14}$ [/hidden-answer]

Try It

Divide the rational expressions and express the quotient in simplest grade:

$\frac{9{x}^{2}-16}{3{x}^{2}+17x-28}÷\frac{3{x}^{2}-2x-8}{{x}^{2}+5x-14}$

[reveal-answer q="fs-id1167339432756″]Bear witness Solution[/reveal-answer]
[hidden-answer a="fs-id1167339432756″]

$1$

[/hidden-answer]

Adding and Subtracting Rational Expressions

Adding and subtracting rational expressions works just like adding and subtracting numerical fractions. To add fractions, we demand to find a common denominator. Permit'due south expect at an example of fraction addition.

$\begin{array}{ccc}\hfill \frac{5}{24}+\frac{1}{40}& =& \frac{25}{120}+\frac{3}{120}\hfill \\ & =& \frac{28}{120}\hfill \\ & =& \frac{7}{30}\hfill \end{array}$

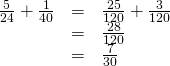
We have to rewrite the fractions so they share a common denominator earlier we are able to add. We must do the same matter when adding or subtracting rational expressions.

The easiest mutual denominator to use will be the least common denominator, or LCD. The LCD is the smallest multiple that the denominators have in mutual. To find the LCD of two rational expressions, we cistron the expressions and multiply all of the distinct factors. For instance, if the factored denominators were $\,\left(x+3\right)\left(x+4\right)\,$ and $\,\left(x+4\right)\left(x+5\right),$ then the LCD would exist $\,\left(x+3\right)\left(x+4\right)\left(x+5\right).$

In one case we notice the LCD, nosotros need to multiply each expression by the form of ane that will change the denominator to the LCD. We would need to multiply the expression with a denominator of $\,\left(x+3\right)\left(x+4\right)\,$ past $\,\frac{x+5}{x+5}\,$ and the expression with a denominator of $\,\left(x+4\right)\left(x+5\right)\,$ by $\,\frac{x+3}{x+3}.$

How To

Given two rational expressions, add or subtract them.

Factor the numerator and denominator.
Find the LCD of the expressions.
Multiply the expressions by a form of 1 that changes the denominators to the LCD.
Add together or subtract the numerators.
Simplify.

Adding Rational Expressions

Add together the rational expressions:

$\frac{5}{x}+\frac{6}{y}$

[reveal-reply q="fs-id1167339429820″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1167339429820″]

First, we have to notice the LCD. In this case, the LCD will be $\,xy.\,$ We then multiply each expression by the appropriate class of 1 to obtain $\,xy\,$ as the denominator for each fraction.

$\begin{array}{l}\frac{5}{x}\cdot \frac{y}{y}+\frac{6}{y}\cdot \frac{x}{x}\\ \frac{5y}{xy}+\frac{6x}{xy}\end{array}$

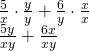
At present that the expressions have the same denominator, we simply add the numerators to observe the sum.

$\frac{6x+5y}{xy}$ [/subconscious-reply]

Analysis

Multiplying past $\,\frac{y}{y}\,$ or $\,\frac{x}{x}\,$ does not modify the value of the original expression because whatever number divided by itself is 1, and multiplying an expression by 1 gives the original expression.

Subtracting Rational Expressions

Subtract the rational expressions:

$\frac{6}{{x}^{2}+4x+4}-\frac{2}{{x}^{2}-4}$

[reveal-reply q="fs-id1167339435145″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339435145″]

$\begin{array}{cc}\frac{6}{{\left(x+2\right)}^{2}}-\frac{2}{\left(x+2\right)\left(x-2\right)}\hfill & \phantom{\rule{2em}{0ex}}\text{Factor}.\hfill \\ \frac{6}{{\left(x+2\right)}^{2}}\cdot \frac{x-2}{x-2}-\frac{2}{\left(x+2\right)\left(x-2\right)}\cdot \frac{x+2}{x+2}\hfill & \phantom{\rule{2em}{0ex}}\text{Multiply each fraction to get LCD as denominator}.\hfill \\ \frac{6\left(x-2\right)}{{\left(x+2\right)}^{2}\left(x-2\right)}-\frac{2\left(x+2\right)}{{\left(x+2\right)}^{2}\left(x-2\right)}\hfill & \phantom{\rule{2em}{0ex}}\text{Multiply}.\hfill \\ \frac{6x-12-\left(2x+4\right)}{{\left(x+2\right)}^{2}\left(x-2\right)}\hfill & \phantom{\rule{2em}{0ex}}\text{Apply distributive property}.\hfill \\ \frac{4x-16}{{\left(x+2\right)}^{2}\left(x-2\right)}\hfill & \phantom{\rule{2em}{0ex}}\text{Subtract}.\hfill \\ \frac{4\left(x-4\right)}{{\left(x+2\right)}^{2}\left(x-2\right)}\hfill & \phantom{\rule{2em}{0ex}}\text{Simplify}.\hfill \end{array}$ [/hidden-answer]

Do we have to use the LCD to add together or subtract rational expressions?

No. Whatsoever common denominator will work, but information technology is easiest to use the LCD.

Try It

Subtract the rational expressions: $\,\frac{3}{x+5}-\frac{1}{x-3}.$

[reveal-answer q="fs-id1167339432621″]Evidence Solution[/reveal-reply]
[hidden-answer a="fs-id1167339432621″]

$\frac{2\left(x-7\right)}{\left(x+5\right)\left(x-3\right)}$

[/hidden-reply]

Simplifying Circuitous Rational Expressions

A complex rational expression is a rational expression that contains additional rational expressions in the numerator, the denominator, or both. We tin simplify complex rational expressions by rewriting the numerator and denominator as single rational expressions and dividing. The complex rational expression $\,\frac{a}{\frac{1}{b}+c}\,$ can exist simplified by rewriting the numerator every bit the fraction $\,\frac{a}{1}\,$ and combining the expressions in the denominator equally $\,\frac{1+bc}{b}.\,$ Nosotros can and then rewrite the expression as a multiplication problem using the reciprocal of the denominator. We get $\,\frac{a}{1}\cdot \frac{b}{1+bc},$ which is equal to $\,\frac{ab}{1+bc}.$

How To

Given a complex rational expression, simplify it.

Combine the expressions in the numerator into a unmarried rational expression by calculation or subtracting.
Combine the expressions in the denominator into a single rational expression by calculation or subtracting.
Rewrite as the numerator divided by the denominator.
Rewrite as multiplication.
Multiply.
Simplify.

Simplifying Complex Rational Expressions

Simplify: $\frac{y+\frac{1}{x}}{\frac{x}{y}}$ .

[reveal-respond q="fs-id1167339259637″]Show Solution[/reveal-respond]
[subconscious-respond a="fs-id1167339259637″]

Begin by combining the expressions in the numerator into one expression.

$\begin{array}{cc}y\cdot \frac{x}{x}+\frac{1}{x}\hfill & \phantom{\rule{2em}{0ex}}\text{ }\text{Multiply by }\frac{x}{x}\text{ to get LCD as denominator}.\hfill \\ \frac{xy}{x}+\frac{1}{x}\hfill & \\ \frac{xy+1}{x}\hfill & \phantom{\rule{2em}{0ex}}\text{ }\text{Add numerators}.\hfill \end{array}$

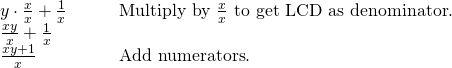
Now the numerator is a single rational expression and the denominator is a unmarried rational expression.

$\frac{\frac{xy+1}{x}}{\frac{x}{y}}$

Nosotros can rewrite this as sectionalization, and then multiplication.

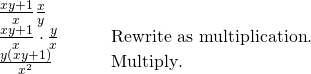$\begin{array}{cc}\frac{xy+1}{x}÷\frac{x}{y}\hfill & \\ \frac{xy+1}{x}\cdot \frac{y}{x}\hfill & \phantom{\rule{2em}{0ex}}\text{Rewrite as multiplication}\text{.}\hfill \\ \frac{y\left(xy+1\right)}{{x}^{2}}\hfill & \phantom{\rule{2em}{0ex}}\text{Multiply}\text{.}\hfill \end{array}$ [/hidden-answer]

Endeavour It

Simplify: $\frac{\frac{x}{y}-\frac{y}{x}}{y}$

[reveal-answer q="fs-id1167339286463″]Bear witness Solution[/reveal-respond]
[subconscious-answer a="fs-id1167339286463″]

$\frac{{x}^{2}-{y}^{2}}{x{y}^{2}}$

[/hidden-answer]

Tin can a complex rational expression always exist simplified?

Aye. Nosotros can always rewrite a complex rational expression as a simplified rational expression.

Key Concepts

Rational expressions can be simplified by cancelling common factors in the numerator and denominator. See (Figure).
We can multiply rational expressions past multiplying the numerators and multiplying the denominators. Come across (Figure).
To divide rational expressions, multiply past the reciprocal of the second expression. See (Figure).
Adding or subtracting rational expressions requires finding a common denominator. Meet (Figure) and (Figure).
Complex rational expressions accept fractions in the numerator or the denominator. These expressions can be simplified. Encounter (Figure).

Department Exercises

Verbal

How tin you use factoring to simplify rational expressions?

[reveal-answer q="fs-id1167339230971″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339230971″]

Yous can gene the numerator and denominator to see if any of the terms can cancel one another out.

[/subconscious-answer]

How do you use the LCD to combine two rational expressions?

Tell whether the post-obit statement is true or false and explicate why: Yous only need to find the LCD when adding or subtracting rational expressions.

[reveal-answer q="fs-id1167339230988″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1167339230988″]

True. Multiplication and division do not require finding the LCD because the denominators can be combined through those operations, whereas addition and subtraction require like terms.

[/subconscious-answer]

Algebraic

For the following exercises, simplify the rational expressions.

$\frac{{x}^{2}-16}{{x}^{2}-5x+4}$

$\frac{{y}^{2}+10y+25}{{y}^{2}+11y+30}$

[reveal-respond q="fs-id1167339199522″]Prove Solution[/reveal-answer]
[hidden-respond a="fs-id1167339199522″]

$\frac{y+5}{y+6}$

[/hidden-reply]

$\frac{6{a}^{2}-24a+24}{6{a}^{2}-24}$

$\frac{9{b}^{2}+18b+9}{3b+3}$

[reveal-respond q="fs-id1167339220319″]Testify Solution[/reveal-reply]
[hidden-answer a="fs-id1167339220319″]

$3b+3$

[/subconscious-reply]

$\frac{m-12}{{m}^{2}-144}$

$\frac{2{x}^{2}+7x-4}{4{x}^{2}+2x-2}$

[reveal-reply q="fs-id1167339428554″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339428554″]

$\frac{x+4}{2x+2}$

[/hidden-answer]

$\frac{6{x}^{2}+5x-4}{3{x}^{2}+19x+20}$

$\frac{{a}^{2}+9a+18}{{a}^{2}+3a-18}$

[reveal-answer q="fs-id1167339226415″]Prove Solution[/reveal-answer]
[hidden-answer a="fs-id1167339226415″]

$\frac{a+3}{a-3}$

[/hidden-reply]

$\frac{3{c}^{2}+25c-18}{3{c}^{2}-23c+14}$

$\frac{12{n}^{2}-29n-8}{28{n}^{2}-5n-3}$

[reveal-respond q="fs-id1167339260411″]Bear witness Solution[/reveal-answer]
[hidden-answer a="fs-id1167339260411″]

$\frac{3n-8}{7n-3}$

[/hidden-answer]

For the following exercises, multiply the rational expressions and express the product in simplest form.

$\frac{{x}^{2}-x-6}{2{x}^{2}+x-6}\cdot \frac{2{x}^{2}+7x-15}{{x}^{2}-9}$

$\frac{{c}^{2}+2c-24}{{c}^{2}+12c+36}\cdot \frac{{c}^{2}-10c+24}{{c}^{2}-8c+16}$

[reveal-reply q="fs-id1167339303701″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339303701″]

$\frac{c-6}{c+6}$

[/hidden-answer]

$\frac{2{d}^{2}+9d-35}{{d}^{2}+10d+21}\cdot \frac{3{d}^{2}+2d-21}{3{d}^{2}+14d-49}$

$\frac{10{h}^{2}-9h-9}{2{h}^{2}-19h+24}\cdot \frac{{h}^{2}-16h+64}{5{h}^{2}-37h-24}$

[reveal-answer q="fs-id1167339239122″]Show Solution[/reveal-respond]
[subconscious-answer a="fs-id1167339239122″]

$1$

[/hidden-answer]

$\frac{6{b}^{2}+13b+6}{4{b}^{2}-9}\cdot \frac{6{b}^{2}+31b-30}{18{b}^{2}-3b-10}$

$\frac{2{d}^{2}+15d+25}{4{d}^{2}-25}\cdot \frac{2{d}^{2}-15d+25}{25{d}^{2}-1}$

[reveal-answer q="fs-id1167339344433″]Testify Solution[/reveal-answer]
[hidden-respond a="fs-id1167339344433″]

$\frac{{d}^{2}-25}{25{d}^{2}-1}$

[/hidden-answer]

$\frac{6{x}^{2}-5x-50}{15{x}^{2}-44x-20}\cdot \frac{20{x}^{2}-7x-6}{2{x}^{2}+9x+10}$

$\frac{{t}^{2}-1}{{t}^{2}+4t+3}\cdot \frac{{t}^{2}+2t-15}{{t}^{2}-4t+3}$

[reveal-answer q="fs-id1167339138936″]Prove Solution[/reveal-answer]
[hidden-respond a="fs-id1167339138936″]

$\frac{t+5}{t+3}$

[/subconscious-reply]

$\frac{2{n}^{2}-n-15}{6{n}^{2}+13n-5}\cdot \frac{12{n}^{2}-13n+3}{4{n}^{2}-15n+9}$

$\frac{36{x}^{2}-25}{6{x}^{2}+65x+50}\cdot \frac{3{x}^{2}+32x+20}{18{x}^{2}+27x+10}$

[reveal-answer q="fs-id1167339428060″]Show Solution[/reveal-answer]
[subconscious-respond a="fs-id1167339428060″]

$\frac{6x-5}{6x+5}$

[/hidden-answer]

For the following exercises, separate the rational expressions.

$\frac{3{y}^{2}-7y-6}{2{y}^{2}-3y-9}÷\frac{{y}^{2}+y-2}{2{y}^{2}+y-3}$

$\frac{6{p}^{2}+p-12}{8{p}^{2}+18p+9}÷\frac{6{p}^{2}-11p+4}{2{p}^{2}+11p-6}$

[reveal-respond q="fs-id1167339314058″]Testify Solution[/reveal-reply]
[subconscious-answer a="fs-id1167339314058″]

$\frac{p+6}{4p+3}$

[/subconscious-answer]

$\frac{{q}^{2}-9}{{q}^{2}+6q+9}÷\frac{{q}^{2}-2q-3}{{q}^{2}+2q-3}$

$\frac{18{d}^{2}+77d-18}{27{d}^{2}-15d+2}÷\frac{3{d}^{2}+29d-44}{9{d}^{2}-15d+4}$

[reveal-answer q="fs-id1167339214028″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339214028″]

$\frac{2d+9}{d+11}$

[/subconscious-answer]

$\frac{16{x}^{2}+18x-55}{32{x}^{2}-36x-11}÷\frac{2{x}^{2}+17x+30}{4{x}^{2}+25x+6}$

$\frac{144{b}^{2}-25}{72{b}^{2}-6b-10}÷\frac{18{b}^{2}-21b+5}{36{b}^{2}-18b-10}$

[reveal-reply q="659011″]Show Solution[/reveal-answer]
[hidden-answer a="659011″] $\frac{12b+5}{3b-1}$ [/hidden-respond]

$\frac{16{a}^{2}-24a+9}{4{a}^{2}+17a-15}÷\frac{16{a}^{2}-9}{4{a}^{2}+11a+6}$

$\frac{22{y}^{2}+59y+10}{12{y}^{2}+28y-5}÷\frac{11{y}^{2}+46y+8}{24{y}^{2}-10y+1}$

[reveal-reply q="fs-id1167339225605″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1167339225605″]

$\frac{4y-1}{y+4}$

[/hidden-answer]

$\frac{9{x}^{2}+3x-20}{3{x}^{2}-7x+4}÷\frac{6{x}^{2}+4x-10}{{x}^{2}-2x+1}$

For the following exercises, add and subtract the rational expressions, and then simplify.

$\frac{4}{x}+\frac{10}{y}$

[reveal-answer q="fs-id1167339317636″]Testify Solution[/reveal-answer]
[subconscious-reply a="fs-id1167339317636″]

$\frac{10x+4y}{xy}$

[/hidden-answer]

$\frac{12}{2q}-\frac{6}{3p}$

$\frac{4}{a+1}+\frac{5}{a-3}$

[reveal-respond q="fs-id1167339317766″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339317766″]

$\frac{9a-7}{{a}^{2}-2a-3}$

[/hidden-answer]

$\frac{c+2}{3}-\frac{c-4}{4}$

$\frac{y+3}{y-2}+\frac{y-3}{y+1}$

[reveal-answer q="fs-id1167339315713″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339315713″]

$\frac{2{y}^{2}-y+9}{{y}^{2}-y-2}$

[/hidden-reply]

$\frac{x-1}{x+1}-\frac{2x+3}{2x+1}$

$\frac{3z}{z+1}+\frac{2z+5}{z-2}$

[reveal-answer q="fs-id1167339315900″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1167339315900″]

$\frac{5{z}^{2}+z+5}{{z}^{2}-z-2}$

[/hidden-reply]

$\frac{4p}{p+1}-\frac{p+1}{4p}$

$\frac{x}{x+1}+\frac{y}{y+1}$

[reveal-answer q="fs-id1167339239322″]Bear witness Solution[/reveal-reply]
[hidden-answer a="fs-id1167339239322″]

$\frac{x+2xy+y}{x+xy+y+1}$

[/subconscious-answer]

For the post-obit exercises, simplify the rational expression.

$\frac{\frac{6}{y}-\frac{4}{x}}{y}$

$\frac{\frac{2}{a}+\frac{7}{b}}{b}$

[reveal-reply q="fs-id1167339437819″]Prove Solution[/reveal-answer]
[hidden-answer a="fs-id1167339437819″]
$\frac{2b+7a}{a{b}^{2}}$ [/hidden-answer]

$\frac{\frac{x}{4}-\frac{p}{8}}{p}$

$\frac{\frac{3}{a}+\frac{b}{6}}{\frac{2b}{3a}}$

[reveal-reply q="fs-id1167339437965″]Prove Solution[/reveal-reply]
[hidden-reply a="fs-id1167339437965″]

$\frac{18+ab}{4b}$

[/subconscious-answer]

$\frac{\frac{3}{x+1}+\frac{2}{x-1}}{\frac{x-1}{x+1}}$

$\frac{\frac{a}{b}-\frac{b}{a}}{\frac{a+b}{ab}}$

[reveal-answer q="fs-id1167339240902″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339240902″]

$a-b$

[/subconscious-answer]

$\frac{\frac{2x}{3}+\frac{4x}{7}}{\frac{x}{2}}$

$\frac{\frac{2c}{c+2}+\frac{c-1}{c+1}}{\frac{2c+1}{c+1}}$

[reveal-reply q="fs-id1167339241076″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339241076″]

$\frac{3{c}^{2}+3c-2}{2{c}^{2}+5c+2}$

[/subconscious-answer]

$\frac{\frac{x}{y}-\frac{y}{x}}{\frac{x}{y}+\frac{y}{x}}$

Existent-World Applications

Brenda is placing tile on her bathroom floor. The area of the floor is $\,15{x}^{2}-8x-7\,$ ft². The area of ane tile is $\,{x}^{2}-2x+1{\text{ft}}^{2}.\,$ To notice the number of tiles needed, simplify the rational expression: $\,\frac{15{x}^{2}-8x-7}{{x}^{2}-2x+1}.$

A rectangle that's labeled: Area = fifteen times x squared minus eight times x minus seven.

[reveal-reply q="fs-id1167339433108″]Bear witness Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339433108″]

$\frac{15x+7}{x-1}$

[/hidden-answer]

The area of Sandy's yard is $\,25{x}^{2}-625\,$ ft². A patch of sod has an expanse of $\,{x}^{2}-10x+25\,$ ft². Split up the two areas and simplify to discover how many pieces of sod Sandy needs to encompass her yard.

Aaron wants to mulch his garden. His garden is $\,{x}^{2}+18x+81\,$ ft². One bag of mulch covers $\,{x}^{2}-81\,$ ft². Divide the expressions and simplify to find how many bags of mulch Aaron needs to mulch his garden.

[reveal-answer q="fs-id1167339433288″]Bear witness Solution[/reveal-reply]
[subconscious-reply a="fs-id1167339433288″]

$\frac{x+9}{x-9}$

[/hidden-reply]

Extensions

For the following exercises, perform the given operations and simplify.

$\frac{{x}^{2}+x-6}{{x}^{2}-2x-3}\cdot \frac{2{x}^{2}-3x-9}{{x}^{2}-x-2}÷\frac{10{x}^{2}+27x+18}{{x}^{2}+2x+1}$

$\frac{\frac{3{y}^{2}-10y+3}{3{y}^{2}+5y-2}\cdot \frac{2{y}^{2}-3y-20}{2{y}^{2}-y-15}}{y-4}$

[reveal-answer q="fs-id1167339299716″]Show Solution[/reveal-respond]
[subconscious-answer a="fs-id1167339299716″]

$\frac{1}{y+2}$

[/hidden-answer]

$\frac{\frac{4a+1}{2a-3}+\frac{2a-3}{2a+3}}{\frac{4{a}^{2}+9}{a}}$

$\frac{{x}^{2}+7x+12}{{x}^{2}+x-6}÷\frac{3{x}^{2}+19x+28}{8{x}^{2}-4x-24}÷\frac{2{x}^{2}+x-3}{3{x}^{2}+4x-7}$

[reveal-answer q="fs-id1167339219508″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339219508″]

$4$

[/hidden-respond]

Affiliate Review Exercises

Real Numbers: Algebra Essentials

For the following exercises, perform the given operations.

${\left(5-3\cdot 2\right)}^{2}-6$

[reveal-answer q="fs-id1167339331113″]Evidence Solution[/reveal-answer]
[hidden-respond a="fs-id1167339331113″]

$-5$

[/hidden-answer]

$64÷\left(2\cdot 8\right)+14÷7$

$2\cdot {5}^{2}+6÷2$

[reveal-reply q="fs-id1167339331203″]Prove Solution[/reveal-answer]
[hidden-answer a="fs-id1167339331203″]

[/hidden-answer]

For the following exercises, solve the equation.

$5x+9=-11$

$2y+{4}^{2}=64$

[reveal-reply q="fs-id1167339331269″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1167339331269″]

$y=24$

[/hidden-answer]

For the following exercises, simplify the expression.

$9\left(y+2\right)÷3\cdot 2+1$

$3m\left(4+7\right)-m$

[reveal-reply q="fs-id1167339331371″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1167339331371″]

$32m$

[/hidden-answer]

For the following exercises, place the number as rational, irrational, whole, or natural. Choose the nigh descriptive reply.

[reveal-answer q="fs-id1167339331401″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1167339331401″]

whole

[/hidden-reply]

$\frac{5}{6}$

$\sqrt{11}$

[reveal-answer q="fs-id1167339432136″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339432136″]

irrational

[/subconscious-answer]

Exponents and Scientific Notation

For the post-obit exercises, simplify the expression.

${2}^{2}\cdot {2}^{4}$

$\frac{{4}^{5}}{{4}^{3}}$

[reveal-answer q="fs-id1167339432227″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339432227″]

$16$

[/hidden-reply]

${\left(\frac{{a}^{2}}{{b}^{3}}\right)}^{4}$

$\frac{6{a}^{2}\cdot {a}^{0}}{2{a}^{-4}}$

[reveal-answer q="fs-id1167339432360″]Show Solution[/reveal-reply]
[subconscious-answer a="fs-id1167339432360″]

${a}^{6}$

[/subconscious-answer]

$\frac{{\left(xy\right)}^{4}}{{y}^{3}}\cdot \frac{2}{{x}^{5}}$

$\frac{{4}^{-2}{x}^{3}{y}^{-3}}{2{x}^{0}}$

[reveal-answer q="fs-id1167339295802″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339295802″]

$\frac{{x}^{3}}{32{y}^{3}}$

[/subconscious-respond]

${\left(\frac{2{x}^{2}}{y}\right)}^{-2}$

$\left(\frac{16{a}^{3}}{{b}^{2}}\right){\left(4a{b}^{-1}\right)}^{-2}$

[reveal-respond q="fs-id1167339295996″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339295996″]

$a$

[/hidden-answer]

Write the number in standard notation: $\,2.1314\,×\,{10}^{-6}$

Write the number in scientific notation: 16,340,000

[reveal-reply q="fs-id1167339296047″]Show Solution[/reveal-answer]
[subconscious-respond a="fs-id1167339296047″]

$1.634\,×\,{10}^{7}$

[/hidden-answer]

Radicals and Rational Expressions

For the following exercises, find the principal square root.

$\sqrt{121}$

$\sqrt{196}$

[reveal-answer q="fs-id1167339296129″]Prove Solution[/reveal-reply]
[hidden-answer a="fs-id1167339296129″]

[/hidden-answer]

$\sqrt{361}$

$\sqrt{75}$

[reveal-answer q="fs-id1167339296174″]Show Solution[/reveal-reply]
[subconscious-answer a="fs-id1167339296174″]

$5\sqrt{3}$

[/subconscious-reply]

$\sqrt{162}$

$\sqrt{\frac{32}{25}}$

[reveal-answer q="fs-id1167339296245″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1167339296245″]

$\frac{4\sqrt{2}}{5}$

[/hidden-answer]

$\sqrt{\frac{80}{81}}$

$\sqrt{\frac{49}{1250}}$

[reveal-answer q="fs-id1167339206434″]Testify Solution[/reveal-answer]
[hidden-reply a="fs-id1167339206434″]

$\frac{7\sqrt{2}}{50}$

[/hidden-answer]

$\frac{2}{4+\sqrt{2}}$

$4\sqrt{3}+6\sqrt{3}$

[reveal-answer q="fs-id1167339206525″]Evidence Solution[/reveal-answer]
[hidden-answer a="fs-id1167339206525″]

$10\sqrt{3}$

[/hidden-respond]

$12\sqrt{5}-13\sqrt{5}$

$\sqrt[5]{-243}$

[reveal-answer q="fs-id1167339206599″]Show Solution[/reveal-respond]
[hidden-respond a="fs-id1167339206599″]

$-3$

[/hidden-answer]

$\frac{\sqrt[3]{250}}{\sqrt[3]{-8}}$

Polynomials

For the following exercises, perform the given operations and simplify.

$\left(3{x}^{3}+2x-1\right)+\left(4{x}^{2}-2x+7\right)$

[reveal-respond q="fs-id1167339206757″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1167339206757″]

$3{x}^{3}+4{x}^{2}+6$

[/hidden-answer]

$\left(2y+1\right)-\left(2{y}^{2}-2y-5\right)$

$\left(2{x}^{2}+3x-6\right)+\left(3{x}^{2}-4x+9\right)$

[reveal-reply q="fs-id1167339297739″]Show Solution[/reveal-respond]
[subconscious-reply a="fs-id1167339297739″]

$5{x}^{2}-x+3$

[/hidden-answer]

$\left(6{a}^{2}+3a+10\right)-\left(6{a}^{2}-3a+5\right)$

$\left(k+3\right)\left(k-6\right)$

[reveal-answer q="fs-id1167339297896″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339297896″]

${k}^{2}-3k-18$

[/hidden-reply]

$\left(2h+1\right)\left(3h-2\right)$

$\left(x+1\right)\left({x}^{2}+1\right)$

[reveal-answer q="fs-id1167339298030″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339298030″]

${x}^{3}+{x}^{2}+x+1$

[/hidden-respond]

$\left(m-2\right)\left({m}^{2}+2m-3\right)$

$\left(a+2b\right)\left(3a-b\right)$

[reveal-reply q="fs-id1167339298181″]Bear witness Solution[/reveal-reply]
[subconscious-respond a="fs-id1167339298181″]

$3{a}^{2}+5ab-2{b}^{2}$

[/hidden-answer]

$\left(x+y\right)\left(x-y\right)$

Factoring Polynomials

For the following exercises, find the greatest common cistron.

$81p+9pq-27{p}^{2}{q}^{2}$

[reveal-respond q="fs-id1167339298332″]Evidence Solution[/reveal-reply]
[subconscious-answer a="fs-id1167339298332″]

$9p$

[/hidden-reply]

$12{x}^{2}y+4x{y}^{2}-18xy$

$88{a}^{3}b+4{a}^{2}b-144{a}^{2}$

[reveal-answer q="fs-id1167339308789″]Testify Solution[/reveal-answer]
[hidden-reply a="fs-id1167339308789″]

$4{a}^{2}$

[/subconscious-answer]

For the following exercises, factor the polynomial.

$2{x}^{2}-9x-18$

$8{a}^{2}+30a-27$

[reveal-answer q="fs-id1167339308882″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1167339308882″]

$\left(4a-3\right)\left(2a+9\right)$

[/hidden-answer]

${d}^{2}-5d-66$

${x}^{2}+10x+25$

[reveal-reply q="fs-id1167339308995″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339308995″]

${\left(x+5\right)}^{2}$

[/hidden-respond]

${y}^{2}-6y+9$

$4{h}^{2}-12hk+9{k}^{2}$

[reveal-respond q="fs-id1167339309109″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1167339309109″]

${\left(2h-3k\right)}^{2}$

[/hidden-answer]

$361{x}^{2}-121$

${p}^{3}+216$

[reveal-answer q="fs-id1167339309204″]Evidence Solution[/reveal-answer]
[hidden-reply a="fs-id1167339309204″]

$\left(p+6\right)\left({p}^{2}-6p+36\right)$

[/hidden-answer]

$8{x}^{3}-125$

$64{q}^{3}-27{p}^{3}$

[reveal-answer q="fs-id1167339309327″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1167339309327″]

$\left(4q-3p\right)\left(16{q}^{2}+12pq+9{p}^{2}\right)$

[/hidden-answer]

$4x{\left(x-1\right)}^{-\frac{1}{4}}+3{\left(x-1\right)}^{\frac{3}{4}}$

$3p{\left(p+3\right)}^{\frac{1}{3}}-8{\left(p+3\right)}^{\frac{4}{3}}$

[reveal-answer q="fs-id1167339433736″]Testify Solution[/reveal-answer]
[hidden-answer a="fs-id1167339433736″]

${\left(p+3\right)}^{\frac{1}{3}}\left(-5p-24\right)$

[/hidden-answer]

$4r{\left(2r-1\right)}^{-\frac{2}{3}}-5{\left(2r-1\right)}^{\frac{1}{3}}$

Rational Expressions

For the following exercises, simplify the expression.

$\frac{{x}^{2}-x-12}{{x}^{2}-8x+16}$

[reveal-answer q="fs-id1167339433980″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1167339433980″]

$\frac{x+3}{x-4}$

[/hidden-answer]

$\frac{4{y}^{2}-25}{4{y}^{2}-20y+25}$

$\frac{2{a}^{2}-a-3}{2{a}^{2}-6a-8}\cdot \frac{5{a}^{2}-19a-4}{10{a}^{2}-13a-3}$

[reveal-answer q="fs-id1167339434201″]Testify Solution[/reveal-respond]
[hidden-answer a="fs-id1167339434201″]

$\frac{1}{2}$

[/subconscious-answer]

$\frac{d-4}{{d}^{2}-9}\cdot \frac{d-3}{{d}^{2}-16}$

$\frac{{m}^{2}+5m+6}{2{m}^{2}-5m-3}÷\frac{2{m}^{2}+3m-9}{4{m}^{2}-4m-3}$

[reveal-respond q="fs-id1167339434421″]Testify Solution[/reveal-reply]
[hidden-reply a="fs-id1167339434421″]

$\frac{m+2}{m-3}$

[/hidden-answer]

$\frac{4{d}^{2}-7d-2}{6{d}^{2}-17d+10}÷\frac{8{d}^{2}+6d+1}{6{d}^{2}+7d-10}$

$\frac{10}{x}+\frac{6}{y}$

[reveal-answer q="fs-id1167339434616″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339434616″]

$\frac{6x+10y}{xy}$

[/hidden-answer]

$\frac{12}{{a}^{2}+2a+1}-\frac{3}{{a}^{2}-1}$

$\frac{\frac{1}{d}+\frac{2}{c}}{\frac{6c+12d}{dc}}$

[reveal-answer q="fs-id1167339434792″]Prove Solution[/reveal-answer]
[hidden-answer a="fs-id1167339434792″]

$\frac{1}{6}$

[/subconscious-respond]

$\frac{\frac{3}{x}-\frac{7}{y}}{\frac{2}{x}}$

Chapter Practice Exam

For the post-obit exercises, identify the number as rational, irrational, whole, or natural. Choose the near descriptive answer.

$-13$

[reveal-answer q="fs-id1167339434892″]Evidence Solution[/reveal-answer]
[hidden-answer a="fs-id1167339434892″]

rational

[/subconscious-respond]

$\sqrt{2}$

For the post-obit exercises, evaluate the equations.

$2\left(x+3\right)-12=18$

[reveal-answer q="fs-id1167339434956″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339434956″]

$x=12$

[/hidden-answer]

$y{\left(3+3\right)}^{2}-26=10$

Write the number in standard notation: $3.1415\,×\,{10}^{6}$

[reveal-respond q="fs-id1167339435052″]Evidence Solution[/reveal-answer]
[hidden-answer a="fs-id1167339435052″]

3,141,500

[/hidden-answer]

Write the number in scientific annotation: 0.0000000212.

For the following exercises, simplify the expression.

$-2\cdot {\left(2+3\cdot 2\right)}^{2}+144$

[reveal-answer q="fs-id1167339342232″]Evidence Solution[/reveal-respond]
[hidden-reply a="fs-id1167339342232″]

$16$

[/hidden-answer]

$4\left(x+3\right)-\left(6x+2\right)$

${3}^{5}\cdot {3}^{-3}$

[reveal-reply q="fs-id1167339342334″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339342334″]

[/hidden-answer]

${\left(\frac{2}{3}\right)}^{3}$

$\frac{8{x}^{3}}{{\left(2x\right)}^{2}}$

[reveal-reply q="fs-id1167339342441″]Prove Solution[/reveal-answer]
[hidden-reply a="fs-id1167339342441″]

$2x$

[/hidden-answer]

$\left(16{y}^{0}\right)2{y}^{-2}$

$\sqrt{441}$

[reveal-answer q="fs-id1167339342526″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339342526″]

[/hidden-answer]

$\sqrt{490}$

$\sqrt{\frac{9x}{16}}$

[reveal-answer q="fs-id1167339342586″]Bear witness Solution[/reveal-answer]
[hidden-respond a="fs-id1167339342586″]

$\frac{3\sqrt{x}}{4}$

[/hidden-answer]

$\frac{\sqrt{121{b}^{2}}}{1+\sqrt{b}}$

$6\sqrt{24}+7\sqrt{54}-12\sqrt{6}$

[reveal-answer q="fs-id1167339342710″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339342710″]

$21\sqrt{6}$

[/hidden-respond]

$\frac{\sqrt[3]{-8}}{\sqrt[4]{625}}$

$\left(13{q}^{3}+2{q}^{2}-3\right)-\left(6{q}^{2}+5q-3\right)$

[reveal-answer q="fs-id1167339342863″]Show Solution[/reveal-respond]
[subconscious-answer a="fs-id1167339342863″]

$13{q}^{3}-4{q}^{2}-5q$

[/hidden-answer]

$\left(6{p}^{2}+2p+1\right)+\left(9{p}^{2}-1\right)$

$\left(n-2\right)\left({n}^{2}-4n+4\right)$

[reveal-answer q="fs-id1167339343039″]Bear witness Solution[/reveal-reply]
[hidden-respond a="fs-id1167339343039″]

${n}^{3}-6{n}^{2}+12n-8$

[/subconscious-answer]

$\left(a-2b\right)\left(2a+b\right)$

For the post-obit exercises, factor the polynomial.

$16{x}^{2}-81$

[reveal-answer q="fs-id1167339343165″]Show Solution[/reveal-answer]
[subconscious-respond a="fs-id1167339343165″]

$\left(4x+9\right)\left(4x-9\right)$

[/hidden-answer]

${y}^{2}+12y+36$

$27{c}^{3}-1331$

[reveal-answer q="fs-id1167339343274″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1167339343274″]

$\left(3c-11\right)\left(9{c}^{2}+33c+121\right)$

[/hidden-respond]

$3x{\left(x-6\right)}^{-\frac{1}{4}}+2{\left(x-6\right)}^{\frac{3}{4}}$

For the post-obit exercises, simplify the expression.

$\frac{2{z}^{2}+7z+3}{{z}^{2}-9}\cdot \frac{4{z}^{2}-15z+9}{4{z}^{2}-1}$

[reveal-answer q="fs-id1167339343547″]Evidence Solution[/reveal-respond]
[hidden-answer a="fs-id1167339343547″]

$\frac{4z-3}{2z-1}$

[/hidden-answer]

$\frac{x}{y}+\frac{2}{x}$

$\frac{\frac{a}{2b}-\frac{2b}{9a}}{\frac{3a-2b}{6a}}$

[reveal-respond q="fs-id1167339343702″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339343702″]

$\frac{3a+2b}{3b}$

[/subconscious-answer]

Glossary

least common denominator: the smallest multiple that two denominators have in common

rational expression: the quotient of two polynomial expressions

brownbeither.blogspot.com

Source: https://opentextbc.ca/algebratrigonometryopenstax/chapter/rational-expressions/

Algebra Review Factoring and Trinomials and Sinplifying Rational Expressions Pachet

Rational Expressions

Learning Objectives

Simplifying Rational Expressions

How To

Simplifying Rational Expressions

Analysis

Try It

Multiplying Rational Expressions

How To

Multiplying Rational Expressions

Endeavor It

Dividing Rational Expressions

How To

Dividing Rational Expressions

Try It

Adding and Subtracting Rational Expressions

How To

Adding Rational Expressions

Analysis

Subtracting Rational Expressions

Try It

Simplifying Circuitous Rational Expressions

How To

Simplifying Complex Rational Expressions

Endeavour It

Key Concepts

Department Exercises

Verbal

Algebraic

Existent-World Applications

Extensions

Affiliate Review Exercises

Real Numbers: Algebra Essentials

Exponents and Scientific Notation

Radicals and Rational Expressions

Polynomials

Factoring Polynomials

Rational Expressions

Chapter Practice Exam

Glossary

0 Response to "Algebra Review Factoring and Trinomials and Sinplifying Rational Expressions Pachet"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel